This post is about Antecons, a product recommendation engine, now part of Conversio. Antecons is no longer commercially available, but I have kept my developer diary on my website with permission.
The first data mining algorithm that was implemented for Antecons was Frequent Pattern growth (FP-growth) which is an algorithm that finds frequent patterns in transactional data such as shopping baskets. Finding frequent patterns is often a necessary step in finding association rules. An association rule is something like “if customers purchase beer, they also buy chips” or “if voter is African American, he/she votes for Barack Obama”. This information can be valuable to analyze patterns and act upon them, e.g. for marketing or reporting.
As mentioned earlier, the first prototype of Antecons was implemented in .NET and used FP-growth to find frequent patterns and association rules. The algorithm was executed in-memory on a single thread. This is fine for smaller datasets but it does not scale to larger datasets. When restarting Antecons, I decided to look at FP-growth again and solve the scaling issue. With the help of MapReduce and Google App Engine, the future is promising.
Before going into detail with the FP-growth and MapReduce, I will briefly give an example of association rule mining. The next section can be skipped if you are familiar with the concepts.
Association rule mining — a quick example
Consider the following dataset consisting of three shopping transactions:
t1 = Beer, Chips, Soda t2 = Chips, Soda t3 = Chips, Soda
From this dataset, we can find frequent patterns. A frequent pattern is a set of one or more items that occur together (frequently) in the dataset. When finding frequent patterns, the support is recorded along with the pattern. The support is simply a count of how many times a pattern occurs in the entire dataset. For the above dataset, we have:
Beer: 1 Chips: 3 Soda: 3 Beer, Chips: 1 Beer, Soda: 1 Chips, Soda: 3 Beer, Chips, Soda: 1
Here, we have defined a minimum support of 1 which means that all patterns with support greater than or equal to 1 are considered frequent.
Based on the frequent patterns, we can construct association rules. As mentioned earlier, an association rule can informally be stated “If customers purchase Chips, they also buy Soda” or a bit shorter:
Chips -> Soda
Association rules have two basic metrics:
- Support: How many times do all the items of a rule appear together in the entire dataset.
- Confidence: How often does the left-hand side of the rule appear with the right-hand side.
Based on the frequent patterns from above, here are a few of the association rules we can construct from those patterns:
Chips -> Soda (support: 3, confidence: 3/3 = 1 = 100%) Beer -> Chips (support: 1, confidence: 1/1 = 1 = 100%) Chips -> Beer (support: 1, confidence: 1/3 = 0.33 = 33%) Beer, Soda -> Chips (support: 1, confidence: 1/1 = 1 = 100%) Chips, Soda -> Beer (support: 1, confidence: 1/3 = 0.33 = 33%)
For more info on association rule mining, see the Wikipedia article for association rule mining.
The problem with association rule mining
Running FP-growth in-memory has certain limitations. To give an idea about the performance, numerous tests of FP-growth were carried out on the prototype of Antecons (when I write FP-growth, I really mean “FP-growth plus finding association rules” but I will just refer to the algorithm as FP-growth). A few of the results are graphed below (please read the caption under the graph).
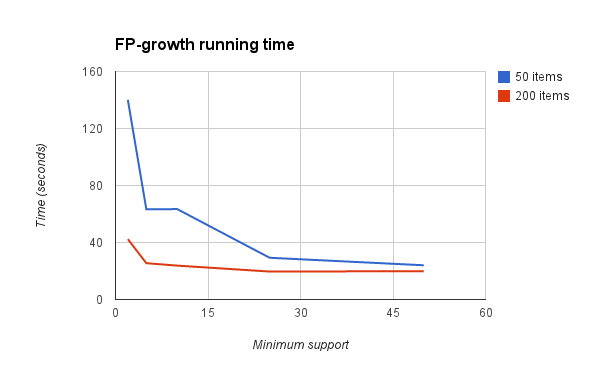
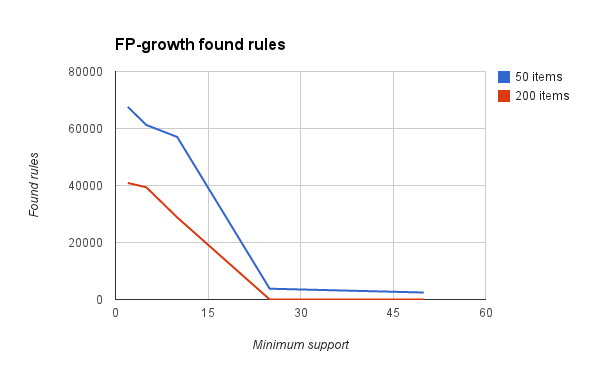
There are two problems here:
- The running time increases as the support decreases.
- The number of association rules decreases as the support increases.
If the goal is to achieve low running time and finding many rules, the above two problems create an unwanted trade-off between running time and number of rules found. In fact, even with 20000 transactions and only 200 unique types of items, 0 rules are found if the minimum support is 50 and only 24 rules are found with minimum support 25. In other words, out of 20000 transactions, it is not possible to find any itemset that occurs 50 or more times. This might be surprising but it actually illustrates one of the main problems with association rule mining:
In order to find interesting association rules, the minimum support for these rules has to be set sufficiently low, but when setting the support very low, the running time and memory usage explodes.
Scaling FP-growth with MapReduce
Some people say that you should not think about scale early on in a project. I agree to some extent but since the limitations of FP-growth start showing on fairly small datasets, it is relevant to consider if the solution can scale at all. When handling millions of transactions, it is no longer feasible to run FP-growth in-memory and on a single thread. Even if we assume that the algorithm scales linearly on the input set, a few minutes all of a sudden turns into a few days and keeping millions of rows in an in-memory data structure is probably not a good idea either.
Fortunately, there are ways to run FP-growth concurrently using a technique called MapReduce. MapReduce is a powerful method that is used extensively by e.g. Google for their search indexing. Google also provides an open source MapReduce framework for Google App Engine — very convenient for Antecons since I chose to deploy on the Google App Engine.
With no prior experience with MapReduce, I was lucky that someone has already implemented FP-growth for MapReduce in Hadoop. Since the basic FP-growth algorithm was implemented a year ago for the Antecons teaser, I just needed a basic idea of how to set up the mapper and the reducer so I chose an approach that is conceptually the same as the one mentioned in the blog post that I just referenced.
The MapReduce pipeline
The full pipeline for creating association rules with MapReduce is actually quite simple and is currently less than 250 lines of code. The first thing that happens is that a reader reads transactions and sends them in batches to the mapper. The map function looks like this:
def fp_map_transactions(transactions):
patterns = fpgrowth.fpgrowth(transactions)
for pattern, support in patterns:
yield pattern, support
After the map step, the MapReduce framework automatically groups together patterns that are the same in the shuffle step which is completely automated. The reduce function receives the pattern and a list of support counts for the pattern so all we have to do is sum the support counts to find the global support count for the pattern:
def fp_reduce(pattern, values):
support = sum([long(i) for i in values])
yield '%s:%s\n' % (pattern, support)
The patterns are yielded to a MapReduce writer that writes the result to the blobstore. After all the results have been stored, another pipeline starts finding the association rules for the patterns. The mapping function for this pipeline receives a pattern-support pair and looks like this:
def fp_to_association_map(line):
pattern, support = line.split(':')
yield pattern, support # Yield the full pattern
if len(pattern) > 1: # Yield every subpattern
for item in pattern:
others = [i for i in pattern if i != item]
yield others, line
Finally, the reducer puts all the things together to create the association rules.
def fp_to_association_reduce(left, values):
# Find value that is not a pattern-support pair
fullpattern_support = [value for value in values
if len(value.split(':')) < 2][0]
values.remove(fullpattern_support)
for value in values:
pattern, support = value.split(':')
for item in left:
pattern.remove(item)
confidence = float(support)/float(fullpattern_support)
rule = { 'left': left, 'right': pattern,
'sup': support, 'conf': confidence }
This works :-)
Initial observations about GAE MapReduce
The standard Datastore reader for the MapReduce framework reads one entity at a time so for step 1, I extended the built-in reader to return batches of transactions instead of just one transaction. Otherwise, FP-growth would run for each transaction in the datastore and that would be silly. The code for this reader is simple and can be found here nowhere (it is not valid as of 2013-05-04).
When starting a MapReduce pipeline on Google App Engine, it can be specified how many shards that the computations should be run in. Theoretically, if the number of shards are set to 16, the computations should run concurrently on 16 different threads. I could not reliably test this on the development server but for 1000 transactions, it took 5 minutes to run the frequent pattern pipeline using 4 shards and 1 minute using 16 shards. This sounds good enough but the framework was reporting that it was only using one of the shards for all computations so the difference in running time is strange. Later, I got the work evenly distributed over all shards and the strange behavior disappeared.
Without much optimization, it currently takes between 1 and 2 minutes to analyze 1000 transactions on 16 shards which is not impressive compared to the in-memory version that could analyze 50000 transactions in 40 seconds but I have not carried out any tests on much larger datasets to see if the MapReduce framework scales. That is next step.
The MapReduce framework for Google App Engine is certainly a great help for easy parallelization of heavy work and I look forward to testing it out more to find out, if it is a good option for more data analysis algorithms.
Thank you for reading.